学术报告一

报告题目：The generalized Newton methods for some nonsmooth optimization problems

报告人：张海斌 教授

报告时间：2023年6月8日（周四）下午15:00-16:30

报告地点：科技楼三楼报告厅

报告摘要：We talk about the Proximal Landweber Newton Method to solve a class of optimization problems with the sparse group LASSO regularization term by the reproducing kernel norm. And then investigate the Semismooth Newton Method for the sparse signal reconstruction problems with several type of noise.

个人简介：张海斌，男，北京工业大学教授，博士生导师。2002年在中国农业大学获博士学位后到北京工业大学理学部任教，先后主持国家自科基金面上项目3项，先后在美国明尼苏达大学、加拿大西蒙弗雷泽大学等知名高校作高级研究学者。近年来在SCI期刊发表学术论文20余篇，出版教材及专著2部.

学术报告二

报告题目：Nonlinear Extrapolation Approximations of π under Dirichlet Distributions

报告人：徐文青 教授

报告时间：2023年6月8日（周四）下午17:00-18:30

报告地点：科技楼三楼报告厅

报告摘要：We construct optimal nonlinear extrapolation estimates of π based on random cyclic polygons generated from symmetric Dirichlet distributions. While the semiperimeter Sn and the area An of such random inscribed polygons and the semiperimeter (and area)Snˊof the corresponding random circumscribing polygons are known to converge to π w.p.1 and their distributions are also asymptotically normal as n→∞,we study in this paper nonlinear extrapolations of the forms

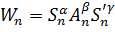and 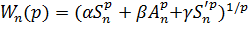where α+β+γ=1 and p≠0.By deriving probabilistic asymptotic expansions with carefully controlled error estimates, we show that Wn and Wn(p) also converge to π w.p.1 and are asymptotically normal. Furthermore, to minimize the approximation error associated with Wnand Wn(p), the parameters must satisfy the optimality condition α+4β-2γ=0. Our results generalize previous work on nonlinear extrapolations of π which employ inscribed polygons only and the vertices are also assumed to be independently and uniformly distributed on the unit circle.

个人简介：徐文青，北京工业大学理学部教授、博士生导师。本科毕业于中国科学技术大学数学系，硕士毕业于中国科学院数学研究所，博士毕业于美国纽约大学库朗数学科学研究所。曾在麻州州立大学和加州州立大学长滩分校从事教学和研究工作多年。研究领域为应用数学及相关交叉学科，在偏微分方程、数值分析、概率及随机过程、编码及信息论等方向发表论文40余篇。